Posts
-
Dynamic-Graph Orientation
tags:Dynamic-Graph Orientation Computer science topics over lunchDynamic-Graph Orientation
1 Orienting Acyclic Graphs
Throughout this post, is an undirected acyclic graph on vertices and edges. The problem we want to solve is called graph orientation:The input is given in the insertion-only streaming model. That is, we know in advance, and the set is being revealed one edge at a time. For each edge that we get, we need to assign a direction (i.e. an orientation), meaning to decide that it either points to or to . When points to we denote it by . Note that when we assign a direction to a new edge, we may as well update the orientation of previously seen edges. When the stream ends, we left with a directed version of , denote it .We are interested in two metrics: the first is the outgoing degree bound, which is defined by the term where is the number of ’s neighbors which points to, in the oriented graph .The second metric is a bound on the orientation cost for a single step of the stream. That is, a bound on the number of edge updates for every time a new edge is being revealed.Due to the fact that is acyclic, we know it is actually a collection of one or more trees, then there exists an orientation in which (think that each node points to its parent in its corresponding tree).2 Orientation Cost
Lets start with a very simple orientation rule: For every step of the stream, let be the edge given in the current step, and . Consider the endpoints of . If belongs to a larger connected component relative to the connected component of , under the graph induced by , then orient to be , otherwise orient it . Note that and cannot be in the same connected component in .Obviously, that update rule has constant orientation cost (in particular it never change the orientations of previous edges). However, the outgoing degree bound is . To prove that, consider some arbitrary vertex . We increase its outgoing degree by when we make it points to another larger connected component. So every time the outgoing degree of increases by , the size of its connected component is at least doubled. Since we have vertices, we cannot double that size more than times.3 Outgoing Degree Bound
Now we will see an update rule that yields a constant degree bound, say :Upon receiving , orient it . Then, if the outgoing degree of exceeds , we apply . This procedure will flip the orientation of any outgoing edge of . Next, check any neighbor that was affected by this change, and apply if it has more than outgoing edges. This process continues recursively until no orientation is changed.Interesting question that immediately pops to mind is, why this process of recursive updates eventually terminates?To see that infinite oscillation is impossible, consider some optimal orientation of , denote it , in which . Suppose that was revealed to the stream, and let be the chain of vertices that we applied to, after orienting it. Denote by the number of edges in that don’t agree with , after applying on . So for example, is the number of conflicting edges right after we inserted but before we start the recursive fixing process, and is the number of conflicting edges after we flip all the outgoing edges of , and so on.We will show that is a strictly decreasing series, and since cannot be negative, that series must terminates. Fix some , which is the number of edges conflicting with before applying . In that moment, , but in the optimal orientation it should be at most , which means that at least of ’s outgoing edges have wrong orientations. So applying adding up to one conflicting edge, but on the other hand, fixing the orientation of at least other edges, thus the total number of conflicting edges with decreased by at least , i.e. .It is immediate that this algorithm yields an orientation with outgoing degree bound of . We now move to show that the amortize orientation cost is also constant. To show that we will use the accounting method, in which we assign positive and negative values to different operations that we perform during processing the stream. As long as those values are constants, if in every step of the stream the aggregated value is non-negative, then we may conclude that the amortize cost per operation is also constant. So suppose that the action of inserting a new edge has a value of , and flipping orientation of an existing edge has a value of . We first prove the following claim.Suppose we got a new edge , and let be the series of vertices that we applied on during the recursive fixing process, after inserting to the graph. Then, all are distinct, and the value of is exactly for any .For the first part, if there is a vertex in appearing twice, it means that we found a cycle in which is impossible. For the second part, assume toward contradiction that we have such that the outgoing degree of was at least 6. It must be due to application on some vertices from , which means that has two neighbors in , and we know that those neighbors are connected, so we found a cycle in and that is a contradiction.It is left to show that at any point in time, the total value of previous operation is non negative. The following claim prove that.For every step, , of the stream, let be the edge revealed on that step. Let be the series of vertices that we applied on during the recursive fixing process, with as defined before. Denote by the aggregated value of all the operations done until inserting (including) and after applying to . Then, for any .By induction on . For , note that and . For , we have and , so using the induction hypothesis, for , assume by induction on that the claim holds, then4 Releasing the Assumptions
This post dealt with a relative simple model, in which the stream only revealing new edges but never deleting a previously seen one. In addition, we assume that our graph is acyclic which is also a very strong assumption. There are works that shows more sophisticated streaming algorithm for fully dynamic graphs (i.e. with edges insertions and deletions), and also works on general graphs that are not necessarily acyclic. Further details can be found in this paper. -
Last TheoryLunch at Weizmann - Cut Equivalent Trees
tags:Last TheoryLunch at Weizmann - Cut Equivalent Trees Computer science topics over lunchLast TheoryLunch at Weizmann - Cut Equivalent Trees
1 Last TheoryLunch Meeting at Weizmann Institute of Science
For those of you who don’t know, this blog originated from my lunch meetings with my friends at Weizmann Institute of Science during my Master studies. As all good things comes to an end, also did my time at Weizmann, and last week our lunch group gathered for the last time. This post presents the topic discussed on that meeting.I want to thank my good friends, Yosef Pogrow and Ron Shiff, for the great time we had and for all the enriching lunch meetings (also those which didn’t include theory). Without you guys, this blog would not have been created, I wish you both best of luck ahead!This post, by the way, contains some results from the research of Yosef Pogrow (who also presented most of the meetings).2 Min-Cuts in a Graph
This post deals with undirected, weighted graphs and cuts on them. We denote by the graph equipped with a weight function on its edges. A cut in this graph is a partition of its vertices to where . For simplicity, we will only mention one of the parts in the partition, usually . Note that it doesn’t matter whether we refer to the first part in the partition , or to the second part , because both parts define the same cut.The value of the cut is defined asA min -cut for a pair is a cut defined by such that note that it is possible that several cuts will satisfy the definition above, but for our purposes they are equivalent (since they all have the same value).Before diving into the theorem about cut equivalent trees, we setup the following notation. For a given tree and any edge , removing that edge from the tree breaks it down into two connected components, one that contains , and another one that contains . Denote the component containing as , and then the other component is exactly . Since the only path connecting and was the removed edge, then is actually the min -cut in (the same is true for since it defines the same cut).A simple fact about trees is, that for any tree and vertices inside it, the min -cut is given by where is the edge with minimum weight along the path that connects and . Since any vertices tree has exactly edges, there are at most unique values of min-cuts that the tree can yield.Cut-Equivalent Trees [Gomory and Hu, 1961]. For any weighted undirected graph there is a weighted tree on the same set of vertices such that:
(a) for any , the value of the min -cut in is equal the value of the min -cut in (with respect to their respective weight functions), and
(b) for any edge , Such trees are known as Cut-Equivalent trees (also known as GH-trees).The proof is omitted from this post, and we move to discuss a nice implication of that theorem: it puts a limit on the number of different min-cut values that a graph can have. Since there are different pairs in a graph there can be potentially unique min-cut values, however, the theorem says that any value of a min-cut in is being represented by a (possibly different) min-cut in , and there are at most min-cut values in , then has at most unique min-cut values.3 General Cuts in a Graph
Until now, we talked about minimum cuts. The theorem above state that for any graph , there is a cut-equivalent tree that can tell us much about all the minimum cuts in . It can tell us all the possible min-cut values that can have, moreover, for any min-cut value , there is a very easy way to find a cut in that have this exact value. All we need to do is to find an edge in the tree that have weight , suppose that edge is , and the desired cut in is given by .One interesting question to ask is, what cut-equivalent trees can tell us about “general” cuts? The answer is given in the following theorem.[Krauthgamer and Pogrow, 2017]. Let be a weighted undirected graph with vertices, and let be a cut-equivalent tree of . Then for anyWe start with the left-hand side. Recall that the value of a cut is the sum of weights of all the “crossing edges”, meaning, edges which have endpoints in both parts of the partition. Then, combined with the second property of the tree, and the fact that for any edge , we get so it is suffice to show that any crossing edge in the sum of the original graph , contributes also to a sum of for some tree-edge such that . So fix some crossing edge ( ) from the original graph, and consider the unique path connecting and over the tree. Since we starting the path with a vertex from and ending with a vertex in , there must be an edge along the path such that and . That edge separates from in the tree, so and . Since then it contributes to , which is what we wanted to prove.
We proceed to show the second inequality. For each in the sum of , we know that since the weight of the tree-edge is equal to the min -cut in , thus in particular smaller or equal to the value of the cut (which also separates from but might not be of minimum weight). The inequality follows by summing over all the crossing edges in over , which is at most edges.4 The Inequalities are Tight
We conclude this post with examples for cases in which one of the inequalities became an equality.For the first inequality, take any graph and a corresponding cut equivalent tree . Fix an arbitrary tree-edge . The cut is the min -cut in and by the first property of the tree .For the second inequality, consider the complete graph on vertices with all its edges weighted . Its cut-equivalent tree must be a star in which every edge weighed . See example of an eight vertices star in the figure below (taken from Wikipedia).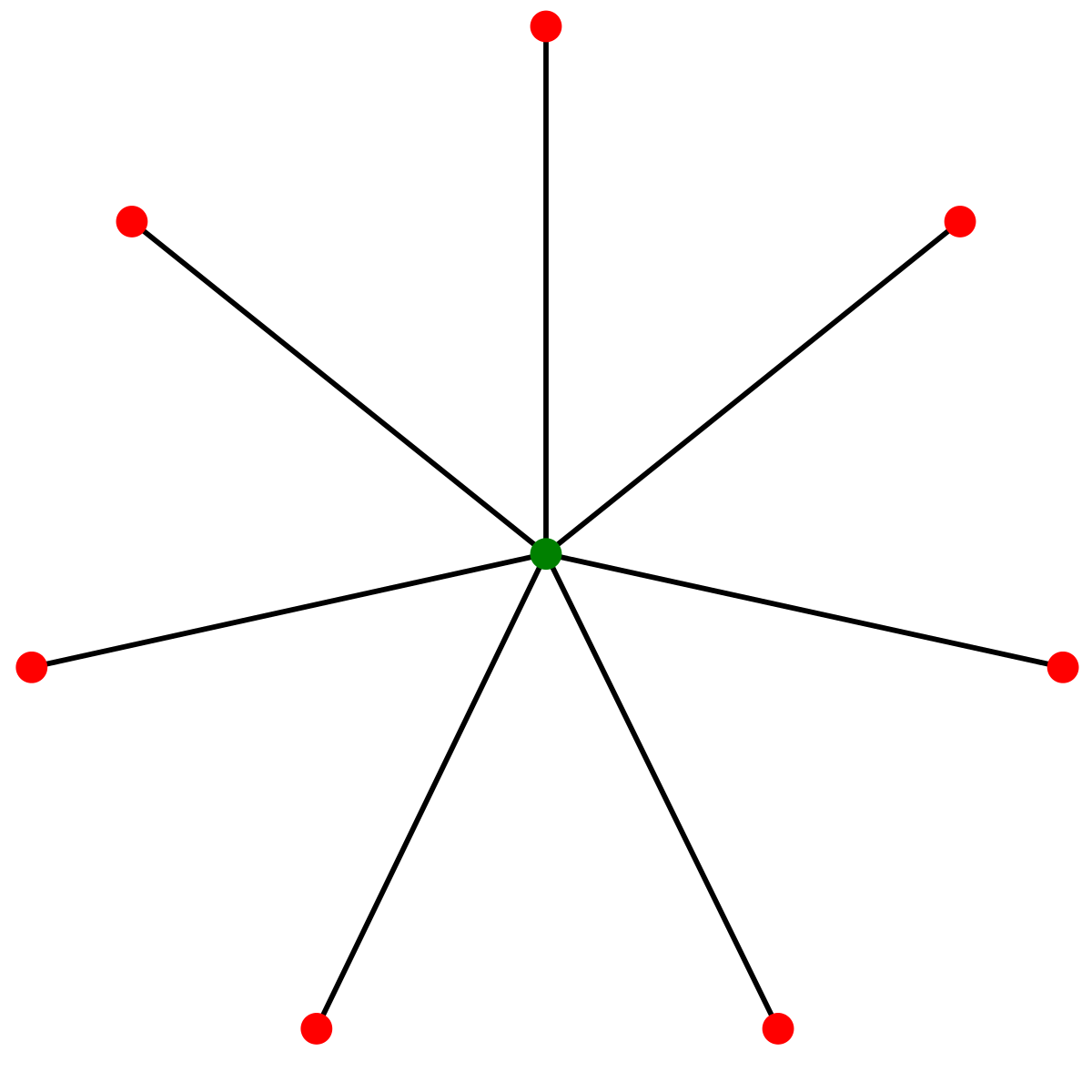 Suppose the vertex in the center of the star is . The cut has weight of over , however, it has weight in the star which is exactly .
Suppose the vertex in the center of the star is . The cut has weight of over , however, it has weight in the star which is exactly . -
On the Hardness of Counting Problems - Part 2
tags:On the Hardness of Counting Problems - Part 2 Computer science topics over lunchOn the Hardness of Counting Problems - Part 2
1 Recap
The previous post discussed the and families. We said that the hierarchy between decision problems from do not preserved when moving to their Counting versions. We defined and formulas (see section 2 in previous post), and the problems CNF-SAT that is -complete and DNF-SAT that is in . We used the relation between their Counting versions to show that and are equally hard to be solved exactly. The relation is as follows: if is a variables formula, then Furthermore, we showed that both problems are -complete, demonstrating that even an “easy” decision problem like DNF-SAT can be very hard when considering its Counting counterpart.This post we will show that there is some hierarchy inside when considering approximated solutions instead of exact solutions.2 Approximation Algorithm for #DNF-SAT
2.1 Deterministic Approximation
Let be a formula, and . We want to find a polynomial time algorithm that yields some which is an approximation for . Formally, for an approximation factor of , . We will talk more about the approximation parameter later.First note that if a clause contains a variable and its negation then immediately we can conclude that there are no satisfying assignments (s.a.) for that clause as it contains a contradiction, so we will omit it from the formula (can be done in linear time). So from now on, assume that do not contain any contradiction. For the rest of this discussion, we say that a boolean variable appear in a clause if either it or its negation contained in .Let’s focus on an arbitrary clause . We can easily count the number of s.a. it has; it is exactly when is the number of variables that do not appear in . That is true because the value of any variable in is determined by its appearance (if it has negation or not) so only variables which are not in can be either or and having two options.Moreover, we can efficiently sample at uniform any s.a. for that clause. Simply iterate over the variables, if a variable appears in then it have only one allowed value so assign it that value, and if it is not appear in then toss a coin and assign or accordingly.Trivial approximation algorithm will calculate the exact for each in and returns their sum . However, we may have s.a. that were counted more than once (if they are satisfying more than a single clause). Thus the approximation factor of that algorithm is , because in the worst case all the clauses have the same set of satisfying assignments so we counted each s.a. times, yielding .We can improve that algorithm by using the inclusion-exclusion principle: instead of accumulating the number of s.a. for each clause, accumulate the number of s.a. that weren’t count so far.Unfortunately, finding which assignment was already counted forces us to enumerate all possible assignments, which obviously takes exponential time. Hence we will give a probabilistic estimation for that, instead. When working with estimations, we need to state the success probability for our estimation and it is also preferable that we will have a way to increase that probability (mostly at the cost of more computations and drawing more random samples).Next section we will describe how to get an estimation of such that for any , even a polynomially small one (i.e. ) with a very high probability.2.2 Probabilistic Approximation
The overall procedure is still simple: iterate over each clause and estimate the fraction of s.a. for that were not counted before (as a number between zero and one), denote that estimation by , let be the total number of s.a. for calculated as mentioned in the deterministic approximation section. Then output .It left to show how to compute , so we do the following. Let , when will be determined later. Sample independent times, an uniformly random s.a. for . For each assignment define a corresponding binary variable that is if it is not satisfying any previous clause, and otherwise. Note that evaluating all takes time. Then return . That completes our probabilistic approximation algorithm for .Analysis
We need to analyze the quality of approximation of each , then show that with high probability is within the claimed approximation bounds. For the first part, we focus on a single estimation for the clause .Let be the number of all s.a. for and let be the number of s.a. for that aren’t satisfying any clause before . Out goal is to show that is, with high probability, close to . Observe that all the variables for estimating were actually sampled i.i.d from a Bernoulli distribution with parameter (which is also its expectation). As a result , so apply Hoeffding inequality to get which means that with high probability the estimator is “successful”, that is, and equivalently, If all the estimators are successful, then and also similarly , which are exactly the approximation bounds that we want to achieve. To conclude the analysis, note that by applying the union bound, all the estimators will be successful with probability .Trade off between the parameters
It is interesting to examine the relation between the different parameters, and how each affect the running time, success probability, and the quality of approximation.Consider the parameter , which is the number of samples the algorithm has to draw to estimate each . That depends linearly on the parameter which controls the “success probability” of all the estimators (simultaneously). On the one hand, large gives a success probability that is extremely close to . But on the other hand, it increase the number of samples per clause, and the total running time of the algorithm, which is .Similarly, the better approximation we want for , the smaller that we should set (even smaller than ), then the number of samples and the running time increase inversely proportional to .3 What About Approximating #CNF-SAT?
Previous section dealt with approximating, either in the deterministic or probabilistic manner, the problem. Unfortunately, as oppose to that we did with exact solutions, approximating do not help us approximating . We will prove that by proving a stronger claim.Let be any -complete problem, and denote its Counting versions. There is no polynomial-time approximation algorithm of to any factor, unless .Assume that . Suppose toward contradiction that we have some polynomial-time approximation algorithm for , and denote it by . Given an instance for the decision problem , simulate and get an approximation for . Then declare as the output of the decision problem if that approximation is zero, and otherwise. Note that this reduction runs in polynomial time. Moreover, the Counting versions have zero solutions if and only if . Since any multiplicative approximation of zero is still zero, we can use the approximation algorithm for the counting problem to efficiently solve the -complete decision problem, contradicting that .4 Formulas are Not Always Easy!
During this and the previous post, we mentioned formulas as something which is easy to solve. We showed that , and always compared it to its “difficult” variation - the version. However, a formula can also be “difficult”. It just depends what we are asking. For example, deciding if a formula is a tautology (i.e. evaluated to for any assignment) is an -complete problem. One can show that by noting that is a formula, and is a instance for CNF-SAT if and only if is a instance for the DNF-TAUTOLOGY problem. Thus, the problem are equally hard.Similarly, we can define an “easy” problem for formulas: decide whether a formula is a tautology can be done in polynomial time, by checking if its negation has a s.a. which is polynomial since and is a formula.As a conclusion, the hardness of those decision problems depends not only on the form of the formula but also on what are we asking to decide. -
On the Hardness of Counting Problems - Part 1
tags:On the Hardness of Counting Problems - Part 1 Computer science topics over lunchOn the Hardness of Counting Problems - Part 1
1 What is a Counting Problem?
Every undergraduate student in Computer Science knows the and families and the legendary question “is equals ?”. However, there is another interesting family that is not always covered in undergraduate courses; that is the (“sharp P”) family. In this post we will define and discuss this family and two concrete similar-but-different problems from it that demonstrate interesting properties about its hardness.Formally, is the family of decision problems that can be solved in polynomial time. A known example is the Perfect Matching problem: given a graph, determine whether it has a perfect matching or not. A perfect matching is a set of edges that touches all the vertices in the graph and any pair of edges have disjoint endpoints.The family contains all the decision problems that has polynomial time algorithm over the non-deterministic computational model (we won’t get into that). We know that , but we don’t know if the other direction also holds. A famous -complete example is the Hamiltonian Cycle problem: given a graph, determine whether it contains a cycle that visits every vertex exactly once. We say “complete” to note that the problem is harder at least as any other problem inside that family, that is, if we could solve it efficiently (i.e. in polynomial time) then we could solve any other problem in the family efficiently. When a problem is at least harder as other problem we denote it .Any problem in either or can be rephrased slightly different. We can ask “how many perfect matching this graph contains?” rather than “is there a perfect matching in this graph?”. When asking how much instead of is there the problem become a Counting problem. Following that, the formal definition of is: the family the Counting version of any problem in .Notice that for any problem we have because having a count of the desired property can, in particular, distinguish between the cases that this count is or higher, that is, decide whether that property exists or not. Hence, we can safely state the general hierarchy, that .Let be the Perfect Matching and Hamiltonian Cycle problems respectively, and let be their Counting versions. It is interesting to see whether the hierarchy between problems from and preserved for their Counting versions as well. For instance, for the problems above, we know that since and is -complete, is that implies also ?The short answer is no. In the next section we will show that in a detailed discussion.2 Counting Makes Problems Much Harder
We start with two basic definitions from the field of boolean logic.A Conjunctive Normal Form ( ) formula other a set of boolean variables is defined as where each of its clauses is of the form , that is, the clause is a disjunction of some number of literals. A literal is a variable or its negation. Note that since there are variables then .A Disjunctive Normal Form ( ) formula other a set of boolean variables is defined analogously to the version, as where each of its clauses is of the form .The CNF-SAT problem, gets as an input a boolean formula, and decides whether that formula has a satisfying assignment (s.a.) or not. That is, an assignment of for each of its variables such that the formula evaluates to . The DNF-SAT is defined the same but for formulas rather than ones.We will need the following facts in the coming discussion:- The operator (negation) transforms any formula to a formula and vice versa.
- For any boolean formula over variables (regardless its form), there are exactly possible assignments each of which satisfy exactly one from .
It is very easy to solve DNF-SAT efficiently, meaning, in polynomial time. Given a formula , iterate over its clauses until you find a satisfiable clause then declare that is satisfiable, however, if you failed to find such a clause then declare that is not satisfiable. Observe that any clause of the form is satisfiable if and only if it does not contains a variable and its negation; which we can check with a single pass over the literals of . As a result, .In contrast to DNF-SAT, the CNF-SAT is know to be -complete, so we believe that it cannot be solved in polynomial time. Similar to the claim from the previous section, we conclude that CNF-SAT is “at least harder” as DNF-SAT, that is, . However, as regard to the Counting versions of those problems, we can show the opposite inequality; that .To prove that, we need to show that if we could solve efficiently, then we could solve efficiently. So suppose we have a magical algorithm that can solve in polynomial time. Given a formula over boolean variables, construct and feed it to the magical algorithm. Let its output be the number , then return .The correctness of that reduction follows from the two facts we stated earlier. Note that also all the procedures can be executed in polynomial time, so we solved in polynomial time using an efficient solver for , therefore, .Actually, if we will look closely on that reduction, we will see that it should work perfectly for the other direction as well, that is, solving by a an efficient algorithm for the , so we may conclude that both problems are equally hard. This is an evidence that the hierarchy between decision problems do not preserved for their Counting versions. Putting it differently, we can say that Counting makes problems much harder, such that even an “easy” problems from become harder as the entire when you consider its Counting version.3 is Also -Complete
Since and are equally hard, it is enough to show that is -complete; for that we need a reduction from any problem in to . Recall the Cook-Levin reduction which proves that CNF-SAT is -complete. That reduction can be applied to any and produce a polynomial procedure that converts any input for the original problem , to a formula for the problem CNF-SAT, such that is satisfiable if and only if the decision problem says for the original input . That way, any efficient solver for CNF-SAT solves efficiently, so .An important property of the Cook-Levin reduction is that it keeps the number of s.a. for exactly as the number of witnesses for the original input of . That means, that we can use the same reduction to convert any Counting problem to . That is, the reduction will yields a procedure to convert any input for to a formula for such that the number of s.a. of is the solution for . As a result, is -complete, and then also .Following the conclusion from previous section, we can say further that even a simple problem from , can have a Counting version that is not just “harder” but harder as any other problem in .4 Is There a Structure inside ?
Going back to the and problems, we saw that they are related via the relation for any formula over boolean variables. We exploited that relation to show that the problems are equally “hard” when talking about exact-solutions. However, an hierarchy emerged once we moved to consider approximated solutions for those problems. Therefore, there is some kind of structure for the family under the appropriate notion of “solving” the problems.Next post we will discuss an approximation algorithm for and the hardness of approximating , showing that the additive relation from above it not enough for constructing an approximation algorithm for based on approximation for . -
Approximation Algorithm for the Steiner Tree Problem
tags:Approximation Algorithm for the Steiner Tree Problem Computer science topics over lunchApproximation Algorithm for the Steiner Tree Problem
1 The Steiner Tree Problem
An instance of the Steiner Tree problem is a connected graph on a set of vertices and edges equipped with a positive weight function . Given a set of terminals , a valid solution is s set that induces a sub-graph in which any pair of terminals is connected. The weight of a solution is defined by , and we want to find a valid solution with minimum weight, usually denoted . Note that since the initial graph is connected there is always a valid solution.Finding an exact optimal solution is NP-Complete. However, there is polynomial time approximation algorithm that yields a factor 2 approximation. We say that a solution is 2-approximation for the problem if for some optimal solution .2 Adding Assumptions “for Free”
Given a graph and weight-function , consider the following construction: Let be a clique on the same set of vertices , that is, . Define the weight function as follows, let be the weight of the shortest path from to in the original . When “shortest path” is defined to be the path with minimum sum of weights among all the simple paths that from to . Furthermore, it worth noting that by its definition, obeys the triangle inequality, meaning that for any triple , if , and then .Fix some , we will show that the weight of any optimal solution for the original instance is exactly the same weight as of any optimal solution for . We will do that by showing two inequalities: let be optimal solutions for the original and the modified instances respectively. Then and .Obviously, the inequality holds, because contains all the edges of and for any edge in its weight over the modified instance have , by the definition of . Therefore, the optimal weight over can only be equal to or smaller than the one of .The other direction is less trivial. Take any and convert it to be a valid solution over the original as follows: for any , if and then add . Otherwise, take all the edges along the shortest path connecting the endpoints of other the original graph and add them to . Note that the entire weight of that path cannot exceeds by the definition of . Therefore we end up with a valid solution , that also have . In conclusion, .The proof above gave us a concrete polynomial-time procedure to convert any valid solution over to a valid solution over such that . From that we can conclude that it is suffice to find a 2-approximation for the “easier” instance and then converts it to a 2-approximation solution for the original instance , note also that the construction of from can be done in polynomial time (for example use Dijkstra's algorithm for computing the shortest paths).In other words, we can assume for free (i.e. without losing anything) that is a clique and have the triangle inequality, and design an approximation algorithm that deals only with such instances.3 Approximation Algorithm for the Easier Problem
Let be a clique, be a weight function that obeys the triangle inequality, and is a set of terminals. Use any known polynomial time algorithm to get a Minimum Spanning Tree (MST) on (for instance, use Kruskal's algorithm), let the edges of that tree be . Output as the approximated solution for the Steiner Tree problem.Putting it differently, we claim that , when is some optimal solution for the Steiner Tree problem for that “easier” instance.And now we will prove that.Let be some optimal solution for the Steiner Tree problem. It must be a tree because otherwise we have a redundant edge such that removing it will decrease the weight of the solution and keep it valid (the terminals will stay connected); in contradiction to the optimality of . Run a Depth First Search (DFS) at the root of , traverse all the nodes in the tree and return back to the root. Memorize all the nodes traversed that way (with repetitions) and denote that sequence . By the way we build , it is a cycle that touches all the vertices of (and maybe also others) and uses twice any edge of , once for the forward pass and once for the backward pass, so it has a length . Suppose that , then we conclude thatDefine the following order on : for any two terminals , we say that comes before if the first appearance of in comes before the first appearance of in . Let be the sequence of ordered terminals, note that it is also defines a path because is a clique, that is, for any . Denote that path .By the triangle inequality, for any pair the weighed subpath in , which is the weight of a single edge, is less or equal to the weighted length in (which may use more than one edge), thus .Since touches all the terminals in exactly once, it has no cycles, hence it is also a spanning tree over the vertices and edges of the clique. Recall that the proposed solution is a minimum spanning tree on , therefore . We conclude that as required. -
Probabilistic Approximation Algorithm for Set Cover
tags:Probabilistic Approximation Algorithm for Set Cover Computer science topics over lunchProbabilistic Approximation Algorithm for Set Cover
1 The Weighted Set Cover Problem
In the Weighted Set Cover (WSC) problem, the input is a triple where is a universe of elements, is a family of sets such that each and , and is a weight function that assigns positive weight to each set in . A solution for the WSC problem is valid if and only if , the weight of the solution is . Note that there is always a valid solution, and the goal in the WSC problem is to find such one with minimum weight.Weighted Set Cover is “hard” in many aspects. First, it is hard to efficiently find the exact solution, that is, the problem is NP-Complete so no time-efficient algorithm is known for it. Moreover, it is also hard to approximate the solution better than a factor. Formally, we said that a solution is a approximation for WSC if , when is an optimal solution with minimum weight. The WSC is hard to approximate in the sense that any approximation for that problem is NP-Complete by itself, and that is for any .In this post we will describe a probabilistic approximation algorithm for WSC which runs in time, and is some positive constant that controls the success probability of the algorithm.2 Equivalent Formulation
We can reformulate the Weighted Set Cover problem as a system of linear equations as follows: For any set define an indicator variable and let , thus if then , and otherwise. The objective is then to minimize subject to the following linear constrainsGiven a solution to that system of equations, we can define the corresponding solution for WSC as . Note that by this construction must be valid, moreover, the weights are the same: , so if is minimal then also . The proof of the other direction (from WSC to the system of equations) is similar.Because the linear-time mapping from any optimal solution of one problem to an optimal solution for the other, we can conclude that solving this system of equations is NP-Hard. However, if we relax the “integer requirement”, i.e. that , then the problem becomes much easier. That is, when for any , that system becomes a convex optimization problem, which we can solved with a polynomial-time algorithm. From now on, we will refer only to the convex version, and denote its (exact) solution as fractional solution.So suppose we have a fractional optimal solution for the linear system . Note that for any optimal solution for WSC, because the convex formulation allows for more possible valid solutions so the minimum weight can only be smaller than of .How do we get from a solution for the WSC? The nice trick here is probabilistic rounding. That is, we will treat each as the probability for selecting .We define the following procedure as an helper function:-
Repeat for
times:
- Initialize .
- Solve the convex optimization version of the WSC to get an optimal fractional solution .
- For each , add it to with probability .
- Let the “solution” for the current iteration be .
- Output
The final algorithm is just applying the procedure independent times, and keeping the candidate solutions , then returning the solution with minimum weight among those candidates.Note that all the procedures above have polynomial time (in and ), therefore the total running time of the algorithm is .3 The Solution is Approximately Optimal
We want to show that with high probability . It is easy to see that for each iteration of the sub-procedure , the intermediate set has expected weight equals to the weight of the optimal fractional solution. Formally, note that the optimal value of all the fractional solutions is the same so we will remove the subscript . Next, we continue to calculate the expected weight of the output solution of the sub-procedure, that is, the weight of the candidateIt left to show that with high probability all the candidates are within the weight bound of , and because is being selected from those candidates, we conclude that it also has . In order to get high probability for a single candidate, we can use Markov’s inequality as follows. Define a “failure” of a candidate as , then the probability of a single candidate to fail is bounded by So with probability of at least the candidate has as required.When considering the final solution , it fails only when all the candidates fail and the probability for that is . So we have high constant probability to get a solution that is approximation for the optimal solution.4 The Solution is Probably Valid
What is the probability that the returned solution is not valid? that is, there is at least one element that is not covered by . We analyze that by first considering an arbitrary element and an intermediate solution of the sub procedure . Suppose that belongs to sets, and for simplicity suppose they are . We know that their corresponding variables have by the requirements of the linear system. The probability to leave all these sets outside is that is, the probability that an intermediate solution will not cover is up to .Next, we calculate the probability that is not covered by a where for some selected candidate . Then it must be that is not covered by any intermediate solution of the procedure , and that will happen with probability . Applying the union-bound on all the elements, we conclude that with probability of at most , the selected candidate will not cover the entire universe. In other words, with at least probability, is a valid solution. -
Repeat for
times:
-
Visualizing high-dimensional data with t-SNE
tags:Visualizing high-dimensional data with t-SNE Computer science topics over lunchVisualizing high-dimensional data with t-SNE
Guest author: thanks to Aviv Netanyahu for writing this post!1 What is visualization and why do we need it?
Before working on a dataset we would like to understand it. After working on it, we want to communicate our conclusions with others easily. When dealing with high-dimensional data, it’s hard to get a ’feel’ for the data by just looking at numbers, and we will advance pretty slowly. For example, common visualization methods are histograms and scatter plots, which capture only one or two parameters at a time, meaning we would have to look at many histograms (one for each feature). However, by visualizing our data we may instantly be able to recognize structure. In order to do this we would like to find a representation of our data in D or D.2 Our goal
Find an embedding of high-dimensional data to 2D or 3D (for simplicity, will assume D from now on).
Formally, we want to learn ( is our data, is the embedding) such that the structure of the original data is preserved after the embedding.3 So why not PCA?
PCA projects high-dimensional data onto a lower dimension determined by the directions where the data varies most in. The result is a linear projection which focuses on preserving distance between dissimilar data points. This is problematic:- Linear sometimes isn’t good enough.
- We claim structure is mostly determined by similar data points.
4 SNE (Hinton&Roweis)
This algorithm for high-dimensional data visualization focuses on preserving high-dimensional ’neighbors’ in low-dimension.Assumption - ’neighbors’ in high dimension have small Euclidean distance. SNE converts the Euclidean distances to similarities using Gaussian distribution: is the probability that is the neighbor of in high-dimension. is the probability that is the neighbor of in low-dimension.
Note - choosing for is done by determining the perplexity, i.e. the effective number of neighbors for each data point. Then , is chosen such that has according number of neighbors in the multivariate Gaussian with mean and covariance matrix .
By mapping each to such that is close as possible to , we can preserve similarities. The algorithm finds such a mapping by gradient descent w.r.t. the following loss (cost) function: where and the initialization of low-dimensional data is random around the origin.Notice the loss function, Kullback–Leibler (KL) divergence, is a natural way to measure similarity between two distributions.
Also notice that this loss puts more emphasis on preserving the local structure of the data. KL-div is asymmetric, so different kinds of errors have a different affect:- Type 1 error: is large (i.e. two points were originally close) and small (i.e. these points were mapped too far), we pay a large penalty.
- Type 2 error: is small (i.e. two points were originally far away) and large (i.e. these points were mapped too close), we pay a small penalty.
This is good, as structure is preserved better by focusing on keeping close points together. This is easy to see in the following example: think of “unrolling” this swiss roll (like unrolling a carpet). Close points will stay within the same distance, far points won’t. This is true for many manifolds (spaces that locally resemble Euclidean space near each point) besides the swiss roll.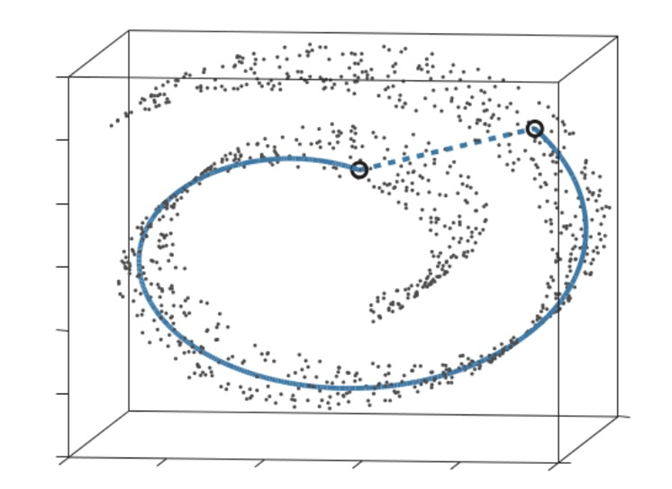
4.1 The crowding problem
The main problem with SNE - mapped points tend to “crowd” together, like in this example: images of 5 MNIST digits mapped with SNE to 2D and then marked by labels This happens because when reducing the dimensionality we need more “space” in which to represent our data-points. You can think of a sphere flattened to a circle where all distances are preserved (as much as possible) - the radius of the circle will have to be larger than the radius of the sphere!On one hand this causes type error (close points mapped too far), which forces far mapped points to come closer together. On the other, causes type error (far points mapped close) which forces them to move away from each other. Type error makes us pay a small price, however if many points cause error , the price will be higher, forcing the points to indeed move. What we just described causes the mapped points to correct themselves to the center such that they end up very close to each other. Consider the MNIST example above. If we did not know the labels we couldn’t make much sense of the mapping.
This happens because when reducing the dimensionality we need more “space” in which to represent our data-points. You can think of a sphere flattened to a circle where all distances are preserved (as much as possible) - the radius of the circle will have to be larger than the radius of the sphere!On one hand this causes type error (close points mapped too far), which forces far mapped points to come closer together. On the other, causes type error (far points mapped close) which forces them to move away from each other. Type error makes us pay a small price, however if many points cause error , the price will be higher, forcing the points to indeed move. What we just described causes the mapped points to correct themselves to the center such that they end up very close to each other. Consider the MNIST example above. If we did not know the labels we couldn’t make much sense of the mapping.5 T-SNE (van der Maaten&Hinton)
5.1 Solving the crowding problem
Instead of mapped points correcting themselves to minimize the loss, we can do this by increasing in advance. Recall, the loss is: , thus larger minimizes it. We do this by defining: using Cauchy distribution instead of Gaussian distribution. This increases since Cauchy distribution has a heavier tail than Gaussian distribution:(Hence the name of the algorithm - Cauchy distribution is a T-student distribution with degree of freedom).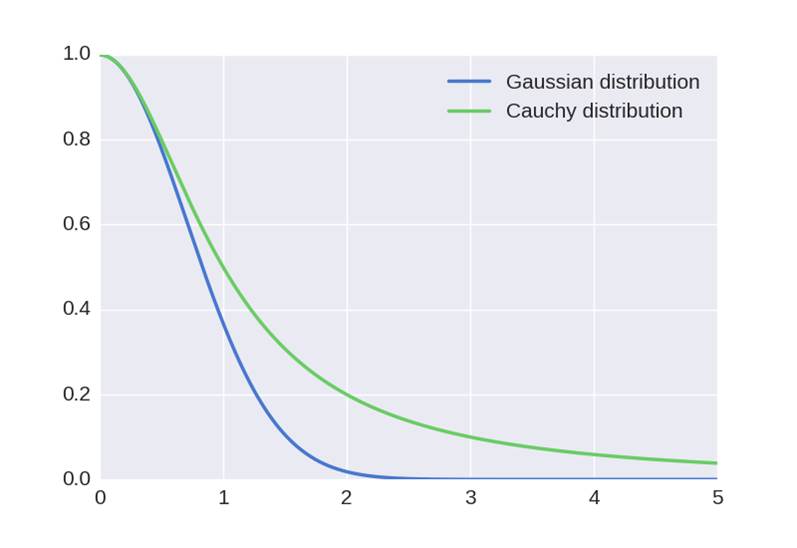 Note also that we changed the probability from conditional to joint probability (this was done for technical optimization reasons). For the same reason, was converted to . We can still use Gaussian distribution for the original data since we are trying to compensate for error in the mapped space.Now the performance on MNIST is much better:
Note also that we changed the probability from conditional to joint probability (this was done for technical optimization reasons). For the same reason, was converted to . We can still use Gaussian distribution for the original data since we are trying to compensate for error in the mapped space.Now the performance on MNIST is much better: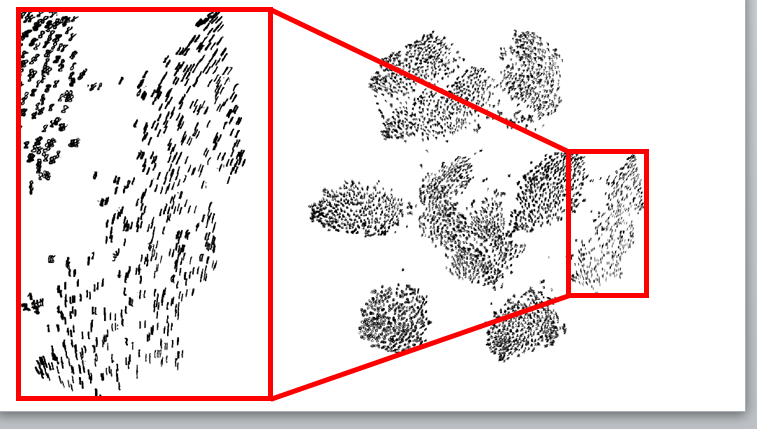 It’s obvious that global structure is preserved and crowding is resolved. Notice also that when zooming in on the mapping of digits, the local structure is preserved as well - digits with same orientation were mapped close to each other.
It’s obvious that global structure is preserved and crowding is resolved. Notice also that when zooming in on the mapping of digits, the local structure is preserved as well - digits with same orientation were mapped close to each other.6 Barnes-Hut approximation (van der Maaten)
Computing the gradient for each mapped point each iteration is very costly, especially when the dataset is very large. At each iteration, , we compute: We can think of as a spring between these two points (it might be too tight/loose depending on if the points were mapped to far/close accordingly). The fraction can be thought of as exertion/compression of the spring, in other words the correction we do in this iteration. We calculate this for mapped points, and derive by all data-points, so for each iteration we have computations. This limits us to datasets with only few thousands of points! However, we can reduce the computation time to by reducing the number of computations per iteration. The main idea - forces exerted by a group of points on a point that is relatively far away are all very similar. Therefore we can calculate where is the average of the group of far away points, instead of for each in the far away group.7 Some applications
- Visualize word embeddings - http://nlp.yvespeirsman.be/blog/visualizing-word-embeddings-with-tsne/
- Multiple maps word embeddings - http://homepage.tudelft.nl/19j49/multiplemaps/Multiple_maps_t-SNE/Multiple_maps_t-SNE.html
- Visualization of genetic disease phenotype similarities by multiple maps t-SNE - https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4243097/
8 When can t-SNE fail?
When the data is noisy or on a highly varying manifold, the local linearity assumption we make (by converting Euclidean distances to similarities) does not hold. What can we do? - smooth data with PCA (in case of noise) or use Autoencoders (in case of highly varying manifold). -
Greedy Algorithm for Multiway-Cut in Trees
tags:Greedy Algorithm for Multiway-Cut in Trees Computer science topics over lunchGreedy Algorithm for Multiway-Cut in Trees
1 The Multiway Cut Problem
The Multiway Cut (MC) problem is a generalization of the known Min-Cut problem. The input is a triple where is an undirected graph with a set of vertices and a set of edges, is the set of terminals, and is a function that assign positive weight to each edge in the graph. A valid cut is a set of edges such that any two vertices are disconnected over the sub-graph . The weight of a given cut is the sum of wights of its edges, that is, . A solution for the MC problem is a valid cut of minimum weight.Let . Note that when the problem is reduced to the regular Min-Cut problem. For general graphs, any makes the problem NP-Hard. However, there are efficient algorithms for Multiway-Cut in trees. A tree is a connected acyclic graph. It is easy to see that if our graph is a tree, any two vertices in it must be connected by exactly one path. Moreover, . We will use these properties later when we prove that the algorithm gives an optimal solution.2 Efficient Algorithm for MC in Trees
Let be the input to the algorithm, and is a tree. To simplify the analysis later on, we will work slightly differently; instead of trying to find a small-weight set to discard from the graph, we will try to find a large-weight set to keep in the graph. Note that obviously and . Therefore, finding with maximum weight is equivalent to finding with minimum weight.The idea is to start with a trivial (and probably not optimal) solution , that is, we don’t keep any edge in the graph such that all the terminals are separated, and we will improve iteratively.We start off with some definitions:A connected component (CC) of a vertex over a graph is the set of all vertices that can be reached from in . Note that if then there are at most CCs in (each vertex has its own CC, which is the case when the graph has no edges).A vertex inside some CC is a master node if it is a terminal vertex. We then say that all the other vertices in that CC are dominated by .Now it is time to describe the algorithm:- Start by sorting the edges of in descending order according to their weights. Let be the ordered sequence such that .
- Initialize a trivial solution . Maintain a set of all the CCs in the resulting graph (each vertex is its own CC).
-
For each
do the following:
- Consider the endpoints of the edge and let be the connected components of respectively. If at least one of them do not has a master node, update and let be the same as but with merged into a new single connected component. Otherwise and .
- Return the set .
3 The Solution is Correct and Optimal
It is easy to see that is a valid solution; we started with all the terminals separated in their own CC, and in each iteration we never connect two CCs that have different masters (i.e. terminals). Therefore, in the returned set, all the connected components has at most one master, meaning that the terminals are separated.The fact that has maximum weight follows by the two following claims:- Any optimal solution has . Moreover, .
- For any iteration of the algorithm, there is an (possibly different) optimal solution such that .
So we conclude that there exists some optimal such that , thus has maximum weight.We move to state and prove those claims formally.Let be the set of all maximum-wight solutions for Multiway-Cut for the instance and is a tree. Then any have . Moreover, .Since we started from a graph that is a tree, the number of CCs in the final sub-graph is exactly , for any . Let be some optimal solution. It left to show that the sub-graph has exactly connected components:
Assume that there are less than , then we must have two terminals which live in the same CC - invalidating the solution . If we assume that there are more than CCs, then we must have a connected component without a master, so we can safely connect it to some other CC with some edge that is not in (and such edge exists since is connected). That way, we get a new valid solution with greater weight than the weight of which is a contradiction.
Similarly, we prove that has CCs: If it has less than , there must be two terminals in the same CCs, and that contradicts the correctness of . If it has more than CCs after iterations, there must be a CC without a master, so we may connect it with some edge, let it be , to other CC without invalidating the solution. But that wasn’t picked when the algorithm considered it - meaning that it could cause a violation in the sub-graph of the th iteration, and since that sub-graph is contained in the sub-graph of the last iteration then we can’t add to our solution - a contradiction.Note that since any optimal solution have exactly CCs, we have that each CC must contains one terminal. So in the final sub-graph defined by the solution, any is dominated by exactly one master mode .Let be the set of all optimal solutions for the instance and in a tree. For any let be the set of optimal solutions such that contained in them. Then, for any , .For we have thus which is not empty. Assume toward contradiction that the claim is false, and let be the smallest such that , so we know that is not empty, and hence . In other words, during the th iteration, the algorithm added the edge to , causing to be empty.
Fix some . Denote and the subgraphs of . From the update rule of the algorithm, at least one of is not dominated by a master over , w.l.o.g assume it is . Let be the master that dominates over , and consider the path connecting , note that any edge along that path belongs to . Since the path does not exists in and in particular in , there is at least one edge that is part of the path and not in , let be such one with minimum weight.
Observe that it is impossible that because it means that the algorithm already rejected on the th iteration and since it was a violation for and then it is also a violation for therefore does not belongs to any optimal solution in , in contradiction that .
So suppose . Note that in the sub-graph induced by , must be dominated my some terminal . Because is a sub-graph of a tree, if then we can close a cycle by adding to , thus . Consider the sub-graph . The edge connects now the terminals and , and that is the only violation in . Since is a sub-graph of a tree there is only one path connecting and and it must contains the path , so removing the edge will break the connection between leading to a valid solution . By the assumption that the weight of can only increase (in fact, the optimality of forces ) and we get an optimal solution that contains , therefore , contradiction.4 Running Time and Similar Algorithms
Note that , so step 1 of the algorithm takes . Step 2 is order of , times the cost of the operations inside the loop. There are data structures such as Union-Find that allow us to track the CCs of the current sub-graph in amortize small running time that is smaller than . Therefore, the total running time is bounded by .Note that the algorithm presented in section 2, is similar to Kruskal’s algorithm for finding the minimum spanning tree. In both cases, the greedy approach leads to an optimal solution. -
Recurrent Neural Network - Recent Advancements
tags:Recurrent Neural Network - Recent Advancements Computer science topics over lunchRecurrent Neural Network - Recent Advancements
1 Last Post of the Series
This post is the last in the series that discussed Recurrent Neural Networks (RNNs). The first post introduced the basic recurrent cells and their limitations, the second post presented the formulation of gated cells as LSTMs and GRUs, and the third post overviewed dropout variants for LSTMs. This post will present some of the recent advancements in the filed of RNNs (mostly related to LSTM units).We start by reviewing some of the notations that we used during the series.We defined to be the family of all affine transformations for any dimensions and , followed by an element-wise activation function , that is,and noted that with the as the activation function, all the functions in are gate functions, that is, their output belongs to .Usually we do not specify and , we assume that whenever there is a matrix multiplication of element-wise operation the dimensions always match, as they are not important for the discussion.2 Variations of the Gate Functions for LSTMs
2.1 Recap: LSTM Formulation - The Use of Gates
LSTM layer is a recurrent layer that keeps a memory vector for any time step . Upon receiving the current time-step input and the output from previous time-step , the layer computes gate activations by applying a the corresponding gate function on the tuple , note that these activations are vectors in .A new memory-vector is then being computed by where is element-wise multiplication and is the state-transition function. The layer then outputs .The gate functions are of great importance for LSTM layer, they are what allow the layer to learn short and long term dependencies, and they also help avoiding the exploding and vanishing gradients problem.2.2 Simple Variations
The more expressive power a gate function have, the better it can learn short \ long term dependencies. That is, if a gate function is very rich, it can account for subtle changes in the input as well to subtle changes in the “past”, i.e. in . One way to enrich a gate function is by making it depends on the previous memory vector in addition to the regular tuple . That will redefine our gate functions family to be for any and diagonal . Such construction can be found in here, note that we can think of as a bias vector that is memory-dependent, thus there are formulation in which the vector is omitted.2.3 Multiplicative LSTMs
In this paper from October 2016, the authors took that idea one step further. They wanted to make a unique gate function for each possible input. Recall that any function in is of the form . For simplicity, consider the case where .We end up with a sum of two components: one that depends on the current input and one that depends on the past (i.e. which encodes information about previous time steps), and the component with larger magnitude will dominate the transition. If is larger, the layer will not be sensitive enough to the past, and if is larger, then the layer will not be sensitive to subtle changes in the input.The author noted that since in most cases the input is an 1-hot vector, then multiply by is just selecting a specific column. So we may think of any gate function as a fixed base affine transformation combined with input-dependent bias vector . That is that formula emphasis the additive effect of the current input-vector on the transition of .The goal in multiplicative LSTM (mLSTM), is to have an unique affine transformation (in our case, unique matrix ) for each possible input. Obviously, if the number of possible inputs is very large, the number of the parameters will explode and it won’t be feasible to train the network. To overcome that, the authors of the paper suggested to learn shared intermediate matrices that will be used to construct an unique for each input, and because the factorization is shared, there are less parameters to learn.The factorization is defined as follow: the unique matrix is constructed by where and are intermediate matrices which are shared across all the possible inputs, and is an operation that maps any vector to a square diagonal matrix with the elements of on its diagonal.Note that the target dimension of may be arbitrarily large (in the paper they chose it to be the same as ).The difference between LSTM and mLSTM is only in the definition of the gate functions family, all the equations for updating the memory cell and the output are the same. In mLSTM the family is being replaced with Note that we can reduce the number of parameters even further by forcing all the gate functions to use the same and matrices. That is, each gate will be parametrized only by and .Formally, define the following transformation such that and then we can define for some fixed learned transformation as in other words, mLSTM is an LSTM that apply its gates to the tuple rather than , and is another learned transformation. If you look again at the exact formula of you will see the multiplicative effect of the input vector on the transformation of . That way, the authors said, can yield much richer family of input-dependent transformations for , which can be sensitive to the past as well as to subtle changes in the current input.3 Recurrent Batch Normalization
Batch normalization is an operator applied to a layer before going through the non-linearity function in order to “normalize” the values before activation. That operator has two hyper-parameters for tuning and two statistics that it accumulates internally. Formally, given a vector of pre-activation values , batch-normalization is where and are the empirical mean and variance of the current batch respectively. and are vectors, and the division in the operator is being computed element-wise. Note that at inference time, the population statistics are estimated by averaging the empirical statistics across all the batches.That paper from February 2017, applied batch normalization also to the recurrent connections in LSTM layers, and they showed empirically that it helped the network to converge faster. The usage is simple, each gate function and the transition function computes when the hyper-parameters and are shared across different gates. Then the output of the layer is . The authors suggested to set because there is already a bias parameter and to prevent redundancy. In addition, they said that sharing the internal statistics across time degrades performance severely. Therefore, one should use “fresh” operators for each time-step with their own internal statistics (but share the and parameters).4 The Ever-growing Field
RNNs is a rapidly growing field and this series only covers a small part of it. There are much more advanced models, some of them are only from few months ago. If you are interested in this field, you may find very interesting stuff here. -
Recurrent Neural Network - Dropout for LSTMs
tags:Recurrent Neural Network - Dropout for LSTMs Computer science topics over lunchRecurrent Neural Network - Dropout for LSTMs
1 Recap
This is the third post in the series about Recurrent Neural Networks. The first post defined the basic notations and the formulation of a Recurrent Cell, the second post discussed its extensions such as LSTM and GRU. Recall that LSTM layer receives vector - the input for the current time step , and the memory-vector and the output-vector from previous time-step respectively, then the layer computes a new memory vector where denotes element wise multiplication. Then the layer outputs where are the forget, input and output gates respectively, and is the state transition function. denotes a family of all affine transformations following by an element-wise activation function , for any input-dimension and output-dimension .In this post, we will focus on the different variants of dropout regularization that are being used in LSTM networks.2 Dropout Regularization
Dropout is a very popular regularization mechanism that is being attached to layers of a neural network in order to reduce overfitting and improve generalization. Applying dropout to a layer starts by fixing some . Then, any time that layer produces an output during training, each one of its neurons is being zeroed-out independently with probability , and with probability it is being scaled by . Scaling the output is important because it keeps the expected output-value of the neuron unchanged. During test time, the dropout mechanism is being turned-off, that is, the output of each neuron is being passed as is.For fully-connected layers, we can formulate dropout as follows: Suppose that should be the output of some layer that has dropout mechanism. Generate a mask , by picking each coordinate i.i.d w.p. from , and output instead of . Note that we hide here the output-scaling for simplicity, and that the mask is being generated any time the layer required to produce an output.At first glance it seems trivial to apply dropout to LSTM layers. However, when we come to implement the mechanism we encounter some technical issues that should be addressed. For instance, we need to decide whether to apply the given mask only to the input or also to the recurrent connection (i.e. to ), and if we choose to apply on both, should it be the same mask or different masks? Should a mask be shared across time or be generated for each time-step?Several works tried to apply dropout to LSTM layers in several naive ways but without success. It seems that just dropping randomly some coordinates from the recurrent connections impair the ability of the LSTM layer to learn long\short term dependencies and does not improve generalization. In the next section we will review some works that applied dropout to LSTMs in a way that successfully yields better generalization.3 Variants
3.1 Mask Only Inputs; Regenerate Masks
Wojciech Zaremba, Ilya Sutskever and Oriol Vinyals published in 2014 a paper that describe a successful dropout variation for LSTM layers. Their idea was that dropout should be applied only to the inputs of the layer and not to the recurrent connections. Moreover, a new mask should be generated for each time step.Formally, for each time-step , generate a mask and compute . Then continue to compute the LSTM layer as usual but use as the input to the layer rather than .3.2 rnnDrop: Mask Only the Memory; Fixed Mask
On 2015, Taesup Moon, Heeyoul Choi, Hoshik Lee and Inchul Song published a different dropout variation: rnnDrop.They suggested to generate a mask for each training sequence and fix it for all the time-steps in that sequence, that is, the mask is being shared across time. The mask is then being applied to the memory vector of the layer rather than the input. In their formulation, only the second formula of the LSTM changed: where if the fixed mask to the entire current training sequence.3.3 Mask Input and Hidden; Fixed Mask
A relatively recent work of Yarin Gal and Zoubin Ghahramani from 2016 also use a make that is shared across time, however it is being applied to the inputs as well on the recurrent connections. This is one of the first successful dropout variants that actually apply the mask to the recurrent connection.Formally, for each training sequence generate two masks and compute and . Then use as the input to the “regular” LSTM layer.3.4 Mask Gates; Fixed Mask
Another paper from 2016, of Stanislau Semeniuta, Aliaksei Severyn and Erhardt Barth demonstrate the mask being applied to some of the gates rather than the input\hidden vectors. For any time-step, generate and then use it to mask the input gate and the second LSTM equation left unchanged.Small note, the authors also addressed in their paper some issues related to scaling the not-dropped coordinates, which won’t be covered here.3.5 Zoneout
The very last dropout variation (to the day I wrote this post) is by David Krueger et al, from 2017. They suggested to treat the memory vector and the output vector (a.k.a hidden vector) as follows: each coordinate in each of the vectors either being updated as usual or preserved its value from previous time-step. As opposed to regular dropout, where “dropping a coordinate” meaning to make it zero, in zoneout it just keeps its previous value - acting as a random identity map that allows better gradients propagation through more time steps. Note that preserving a coordinate in the memory vector should not affect the computation of the hidden vector. Therefore we have to rewrite the formulas for the LSTM layer: given and . Generate two masks for the current time-step . Start by computing a candidate memory-vector with the regular formula, and then use only some of its coordinates to update the memory-vector, that is, Similarly, for the hidden-vector, compute a candidate and selectively update Observe again that the computation of the candidate hidden-vector is based on therefore unaffected by the mask .4 More and More and More
In the last year, dropout for LSTM networks gained more attention, and the list of different variants is growing quickly. This post tried to cover only some fraction of all the variants available out there. It is left for the curious reader to search the literature for more about this topic.Note that some of the dropout variations discussed above can be applied to basic RNN and GRU cells without much modifications - please refer to the papers themselves for more details.Next post, I will discuss recent advancement in the field of RNNs, such as Multiplicative LSTMs, Recurrent Batch Normalization and more. -
Recurrent Neural Network - LSTM and GRU
tags:Recurrent Neural Network - LSTM and GRU Computer science topics over lunchRecurrent Neural Network - LSTM and GRU
1 Recap
The first post in the series discussed the basic structure of recurrent cells and their limitations. We defined two families of functions, the first is which contains all the affine transformations for any and followed by an element-wise activation function And another family which is some kind of extension of in the sense that the input space is rather than Formally, the definition of is In this post, which is the second in the series, we will focus on two activation functions: and . Next section describes what are gate functions, then we move to review two common improvements to the basic recurrent cell: the LSTM and GRU cells.2 Gate Functions
Recall that recurrent layer has two steps. The first is updating its inner state based on both the current input and the previous state vector, then producing an output by applying some other function to the new state. So the input to the layer at each time step is actually the tuple .A gate is a function that takes such a tuple and produces a vector of values between zero and one. Note that any function in and in is actually a gate because of the properties of the and functions. We add gates into a recurrent neuron in order to control how much information will flow over the “recurrent connection”. That is, suppose that is the layer’s current state that should be used at the next time step, a gated layer will use the vector instead of using (when the symbol denotes element-wise multiplication). Note that any coordinate in is a “moderated” version of the corresponding coordinate in because each entry in the gate’s output is in We will see a concrete example in the next section.3 LSTM Cell
Long Short Term Memory Cell (LSTM cell) is an improved version of the recurrent neuron that was proposed on 1997. It went through minor modifications until the version presented below (which is from 2013). LSTM cells solve both limitations of the basic recurrent neuron; it prevents the exploding and vanishing gradients problem, and it can remember as well as it can forget.The main addition to the recurrent layer structure is the use of gates and a memory vector for each time step, denoted by . The LSTM layer gets as inputs the tuple and the previous memory vector then outputs and an updated memory vectorHere is how an LSTM layer computes its outputs: it have the following gates named the forget, input and output gate respectively, and a state-transition function . It first updates the memory vector and then computes Those equations can be explained as follows: the first equation is an element-wise summation of two terms. The first term is the previous memory vector moderated by the forget gate. That is, the layer uses the current input and previous output to determine how much to shrink each coordinate of the previous memory vector. The second term is the candidate for the new state, i.e. moderated by the input gate. Note that all the gates operate on the same input tupleThe input and forget gates control the long-short term dependencies (i.e. the recurrent connection), and allow the LSTM layer to adaptively control the balance between new information that come from the state-transition function and the history information that comes from the memory vector, hence the names for the gates: input and forget.Another difference is that LSTM layer controls how much of its inner-memory to expose by using the output gate. That is being formulated in the second equation.The addition of gates is what preventing the exploding and vanishing gradients problem. It makes the LSTM layer able to learn long and short term dependencies at the cost of increasing the number of parameters that are needed to be trained, and that makes the network harder to optimize.4 GRU
Another gated cell proposed on 2014 is the Gated Recurrent Unit (GRU). It has similar advantages as the LSTM cell, but fewer parameters to train because the memory vector was removed and one of the gates.GRU has two gate functions named the update and reset gate respectively, and a state transition The input to GRU layer is only the tuple and the output is computed as follow: first the layer computes its gates for the current time step, denoted by for the update gate and by for the reset gate. Then the output of the layer is with all the arithmetic operations being done element wise.The term is a candidate for the next state. Note that the state-transition function accepts the previous state moderated by the reset gate, allowing it to forget past states (therefore the name of the gate: reset). Then the output of the layer is a linear interpolation between the previous state and the candidate state, controlled by the update gate.As oppose to the LSTM cell, the GRU doesn’t have an output gate to control how much of its inner state to expose therefore the entire state is being exposed at each time step.Both LSTM and GRU are very common in many recurrent network architectures and achieve great results in many tasks. LSTMs and GRUs can learn dependencies of various lengths which make the network very expressive. However, a too expressive network can leads sometimes to overfitting, to prevent that it is common to use some type of regularization, such as Dropout.Next post I will discuss the dropout variations that are specific for RNNs. -
Recurrent Neural Network - Introduction
tags:Recurrent Neural Network - Introduction Computer science topics over lunchRecurrent Neural Network - Introduction
1 The First Post in the Series
Recurrent Neural Network (RNN) is a neural network architecture that leads to state of the art results in many tasks, such as machine translation, speech recognition, image captioning and many more. Because it is a rapidly evolving field, it is difficult to find all the information (both basic and advanced material) in one place, so I decided to write a series of posts that will discuss Recurrent Neural Networks from their basic formulation to their most recent variations.This post, as the first in the series, will present the concept of a recurrent neuron and its limitations. Next posts will discuss gated neurons like LSTM and GRU, variants of dropout regularization for RNNs and some advanced stuff that I found interesting (bi-directional RNN, Multiplicative LSTM and etc).The next section is dedicated to review the notations and basic terminology that will be used during the entire series. I will assume that the reader is familiar with the basics of neural network (fully connected architecture, back-propagation algorithm, etc). If you are not familiar with one of those concepts, I strongly recommend to review them online before going further. Those notes provides concise introduction to the field. There is also an excellent video-lecture (in Hebrew) by Prof. Shai Shalev-Shwartz from 2016. If you really want to dive deeper, you can find broad introduction in Chapter 6 in Deep Learning book (legally free electronic version here).2 Notations and Basic Terminology
Artificial Neural Network (ANN) is a mathematical hierarchal model inspired from neuroscience. The basic computation unit is a neuron, which is a function from to , where are the input and weight vectors respectively, and is the bias. The function is a non-linear activation function , for example or . Note that a neuron can ignore some of its input coordinates by setting their corresponding entries in its weight vector to zero.Neurons are organized within layers. In the very basic ANN architecture, called a fully connected (FC) neural network, a layer is just a collection of neurons that will be computed in parallel (meaning that they are not connected to each other). For any layer , each of its neurons accepts as inputs all neurons from layer .A layer in FC architecture can be formulate mathematically as a function from to such that where each is a function of a neuron as defined above, with its own weight vector and a bias scalar. The formulation can be simplified using matrix notations: where contains in the i-th row the weight vector of , and is the bias of . The function is the same as before but since its input is now a vector, it apply element-wise on each coordinate of the input, producing an output vector of the same length.We denote the family of all possible FC functions based on some fixed activation function as that family contains all possible layers for any input\output dimension. For abbreviation, I will not mention the dimensions of layers or the specific activation function when they are not important for the discussion.Applying several layers sequentially yield a feedforward FC neural network. That is, given , a FC network with layers is where for some fixed .The number of layers in the network is its depth, and the size of the layers is its width (assuming all the layers are of the same dimension). Training the network is optimizing all the weight matrices and bias vectors such that the network will approximate some target (usually unknown) function. We can think of the optimization process as a process of iteratively updating the choice of layer functions from the family .The FC architecture is simple, yet yields a very powerful model. When wide enough, even a single hidden layer network can approximate to any arbitrary precision almost any continuous function (under some mild assumptions). However, for some tasks it might not be optimal, and different architectures are being used, instead of the FC one.3 The Need for Context
There are tasks that require some notion of context in order to make a decent prediction. For example, tasks that involve time-steps can consider the history until the current time step as a context (a.k.a time-series tasks). For concrete example, consider predicting the next word in a given sequence. Each word has as a context all words preceding it. Note that there are more ways to define the notion of a context, and it mostly depends on the task in hand. For didactic purposes we will focus on the example of next-word prediction.How can we build a model for next-word prediction using FC neural network?The obvious answer is to fix some window size , and build a network that gets the last words in the sentence as features, in order to predict the next word. One immediate limitation of this approach is that the window size is the same for all the examples in the training set, and it is not simple to find a suitable window size. On the one hand, choosing small window may cause the model to miss some important long term relations between words that are more than steps apart (for sentences longer than ). On the other hand, choosing very large increases the number of parameters in the model, which make the optimization harder, and increase the computation time per example, which affect both training-time and prediction-time.Another limitation is that FC layers regards their inputs as ordered information. That is, a FC layer assigns a specific weight for each coordinate in its input vector, causing the order of the features to be meaningful. But in some tasks the order of the features may vary, for example, the subject of a sentence doesn’t limit to specific location inside an English sentence. If we want FC layer to account for that, we have to get a lot of examples (and they need to cover all different cases).What we would like to have here is called parameter sharing. We will come back to that term later in this post.4 Recurrent Cell - Learning to Remember
We want our network to be able to remember information about previous invocations (i.e. the past inputs). In order to do that, our network have to maintain a state. So we need to extend our neuron formulation to include another variable, , that will be its state and be kept during consecutive invocations.That state variable is usually initialized to be zero so that it doesn’t affect the first computation.We will use an upper-script to denote the time step, so is the state of a neuron at time . Since the neurons need to pass information to themselves (i.e. their state from previous invocation) they become recurrent neurons, a.k.a recurrent cells.Recurrent neuron uses internally two functions. The first function updates the inner state based on current input and previous state, which is the transition from time to time , is a new parameter denoting the weight for the previous state.And the second function is for computing the output of the neuron at current time , based on its new state with as the weight and bias of the computation respectively.We can move again to matrix notations to denote several parallel recurrent cells that forms a recurrent layer. The first function updates the vector of states for the entire layer and the second function for computing the output of the layer based on the current state When we come to compare that to the FC formulation, we see that actually the function itself hasn’t changed, but now it accepts as input the state of the layer , rather than the input to the layer . Another change is that before the layer computes its output, it first update its hidden state.Note that we can extend the definition of the family to contains functions like the state-transforming function , by making each accepts two vectors as input instead of one (and we also need another weight matrix for the second input). So denote the family of all hidden-state transition functions as usually the activation function is . We will use that family later on, when discuss gated units as LSTM and GRU.5 Comparing the Architectures - an Example
Consider again the next-word prediction problem. Suppose we have an ordered dictionary that contains the entire vocabulary we will ever need. We will represent any word by an integer indicating its index in the dictionary. In this section we will construct two single-neuron networks, once using the FC architecture and once using the Recurrent architecture.FC network for next-word prediction: Let the window size be . The input to the network can be represent as a vector and the output as . The FC network amounts to for some that maps from to .Recurrent neural network (RNN), however, leads to different representation: the input and the output both integers so the state transition function and the output function are both from to . The idea of the recurrent architecture is to apply the same recurrent layer several times on different inputs (each input from different time-step) in order to get a prediction.Here is a detailed description of how to do that: we take a series of three consecutive words from the beginning of a sentence: and a target next word: . First, feed the network with , it updates the inner state from to some hidden state and outputs . We ignore that output and feed the next word , the network updates its state to and produces that is also ignored. Lastly, we feed to the network, the inner state is being updated to and another output is produced which is now considered as the prediction of the network. Note that in each invocation of the network, the output depends on both the current input and the previous state, therefore is the result of the entire history and (which was initialized to zero).At first glance it looks like there is no meaningful differences between the architectures. We have an implicit sliding window over the words in the sentence for the recurrent neuron rather than explicit sliding window as with the FC neuron. Moreover, the output of FC neuron also depends on all previous time steps because the input is just the values of .However, note that in the FC architecture, each word in the input vector has its own weight and bias whereas in recurrent architecture we use the same weights over and over again (by applying the same function). In other words, in recurrent layers we share the parameters across time. The formula below demonstrate how we applied the same function to updates the hidden-state across different time steps then making a prediction using some on the current state Parameter sharing has a very powerful effect on the learnability of the network both because it reduces the number of parameters that needed to be optimized and it make the network robust to small changes in the context (recall the example about the order of features in the input). In addition, the recurrent layer practically has a dynamic window size. Going back to our next-word prediction network, we can continue to apply the network on consecutive inputs, teaching it dependencies between words that are further than 3 time steps.Note that in our example, we ignored the “intermediate” predictions of the network: and , but we could keep them and feed them as inputs to another recurrent layer making our RNN network deeper. We will discuss it in a later post.6 Limitations of Recurrent Cells
Unfortunately, RNNs are not perfect and maintaining memory is not enough, sometimes the networks needs to be able to forget, for instance, when predicting next-word in a sentence the network needs to reset its state once it reach the end of the sentence.Furthermore, parameter sharing has a serious drawback. Recall that applying the network for multiple time steps leads to a composition of the same upon itself times, something like this which may cause the gradient during back-propagation to either explode or vanish. This problem is known as the vanishing and exploding gradients. In order to get an intuition about that, we make the following simplifications: assume that the activation function inside is the identity instead of , and for all . Suppose that is given to us and it is not all zeros (that is, it encodes some information about the past).We have that so applying the recurrent neuron for time steps amounts to . What happen to as increases? it easier to see the answer when considering the scalar case. If was a real positive number, then either when , or when . The same goes with matrices, suppose has an eigenvalue decomposition such that for orthogonal , so causing the small entries on the diagonal of to vanish, and the large entries to explode. Since the gradients in our network are being scaled according to , they are either explode or vanished. The problem with very large gradients is that they cause the network to diverge (large updates to the parameters), on the other hand, very small gradients cause infinitesimally small updates to the parameters which prevent the network from learning. That is describe much more formally and rigorously here.Next post I will discuss two popular improvements to the recurrent neurons that helps avoid the limitations above: the LSTM and GRU cells.Acknowledgments: I want to thank Ron Shiff for his useful comments and corrections to this post. -
Memory Efficient Algorithm for Finding Cycles in Graphs
tags:Memory Efficient Algorithm for Finding Cycles in Graphs Computer science topics over lunchMemory Efficient Algorithm for Finding Cycles in Graphs
1 Cycle Detection in Graphs
Somewhere in 2015, I encountered a nice algorithmic question during an interview for an algotreading company. The question was how one can decide if there is a cycle in an undirected connected graph? There are two immediate answers here, the first is running Breadth First Search (BFS) on arbitrary node and memorizing the nodes that were already visited. The search ends either when the algorithm complete scanning the whole graph or when it reaches some node twice, outputting “No” or “Yes” respectively. Another possible solution is by running Depth First Search (DFS) and keeping a variable to count the length of the longest path explored. The algorithm declare a cycle if at any point in time the length of the path reaches the number of vertices in the graph. For the rest of this post, denote that number by .Those two solutions are simple, and more important for this discussion, have the same space complexity. That is, both consume around the same amount of working memory (in bits) ignoring the memory needed for the input and output of the algorithm. Even though DFS have implementation that requires less memory than BFS, ultimately both requires bits. One can (informally) justify the aforementioned space complexity as follow: both algorithms have to keep track of their search (a queue in BFS and a stack is DFS) which potentially can be as large as the entire graph thus , and each node need bits for encoding so the total space complexity is bits.During the rest of this post we will focus on space complexity rather than time complexity. We will present an algorithm that can determine if there is a cycle in bits [base on this paper] and then discuss the importance of related problem: the s-t connectivity.2 The s-t Connectivity Problem
2.1 Solving s-t connectivity as a Sub-step
We will start from solving a slightly different problem then uses its solution as a procedure in our cycle-detection algorithm.Introducing the undirected s-t connectivity problem: The input is an undirected graph of size and two vertices . The output should be if there is path in that connects and , and otherwise. The directed s-t connectivity is about the same but the input graph is directed (i.e its edges has directions) and the output should be whether there is a directed path from to .Before we present the algorithm, we first define the following predicate: for any and define if exists a path from to of at most steps (i.e. edges), otherwise .The next observations are key points needed to solve the s-t connectivity efficiently (both for directed and undirected case).- For any and any , we have that if and only if such that and
- Let , they are connected if and only if
From here the algorithm is straightforward: denote the algorithm by that upon receiving from the graph and :- If , it outputs , and if it outputs
- For each : if and then output
- Output
The solution for s-t connectivity can be achieved by outputting “Yes” if and only if .Obviously, the depth of the recursion is and in each level of the recursion the algorithm only needs to keep track of and , which is bits, therefore the total memory complexity of the algorithm is bits.2.2 Extending the algorithm to detect cycles
How solving the s-t connectivity problem helps us with cycles detection? The next observation answer that: let be the graph in question and two endpoints of some edge, they must stay connected after removing that edge from if and only if both participating in a cycle contained in .For the directed case the algorithm is as follow: iterate over any edge , delete it temporarily from and check if on the resulting graph, that is, if is still connected to even after you delete the edge from to . If then declare a cycle, else, restore back the edge and continue to the next one. Note that this solution also works for undirected graphs. The memory complexity is and we done.2.3 Is it the best we can do?
Actually, for undirected graphs there is an algorithm with bits, improving the square on the log in the construction from previous section. The curious reader can read more about it here. For the directed case it is an open question whether we can improve the or not.2.4 Beyond Cycles in Graphs
The directed s-t connectivity problem is an important theoretical problem because it captures the “hardness” of any problem that requires logarithmic amount of memory space. The reduction to show that is actually very easy, suppose we have an algorithm that solves some problem in space where is logarithmic in (and is the size of the input), generate the following directed graph: create a vertex for any state (memory configuration) of the algorithm. Since its memory is , there are at most states (thus vertices). Create an edge from to iff is a valid possible successor state of . Add a vertex and connects to it all the states that leads to outputting “Yes”. Denote by the starting-state of the algorithm and now solving the original problem is equivalent to finding a directed path from to in the states-graph.This reduction was presented by Walter Savitch in 1970, and it also works for Nondeterministic algorithms. The conclusion is that any nondeterministic problem that can be solved in space (where is logarithmic in the size of the input) can be solved deterministically in . Combining that conclusion with the algorithm for directed s-t connectivity yields that any problem with nondeterministic space complexity can be solved deterministically (via reduction to directed s-t connectivity) with space complexity. -
Derandomization for Pairwise Independent Seed
tags:Derandomization for Pairwise Independent Seed Computer science topics over lunchDerandomization for Pairwise Independent Seed
1 Randomized Algorithm Settings
Randomized algorithm is an algorithm that in addition to its inputs also uses internally coin-tosses (i.e. uniformly random bits) in order to decide on its output, so different invocations of the algorithm with same inputs may yield different outputs that depend on the results of these coins. One can think about the internal coin-tosses as a binary string of length that is being fixed before the algorithm starts and being consumed sequentially during the algorithm’s execution. Such string is often called seed, and the randomness within the algorithm now comes from choosing a different string at the beginning of each execution.Note that tossing fair coins, is exactly like drawing uniformly at random a string from the set (i.e. each string has a probability of ).Suppose we have a randomized algorithm that solves a problem of interest. We have a guarantee that for any input of length , algorithm runs in , and outputs either a valid solution if it succeeds or output . The success probability of the algorithm is (which may be even infinitesimally small).The first question to ask is, can we convert the randomized algorithm into a deterministic one?2 Brute Force Derandomization
The answer is yes, and there is a simple way to do that: Upon receiving an input , iterate over all possible strings and run . That is, simulate on with as the random seed. Return the first solution that outputs (i.e. anything that is not ).The idea behind this method is that if there is a non-zero probability for to output a valid solution for the input , then there must be a random seed that leads to that output when executing algorithm on . So all we need to do is iterating over all possible seeds of length , and that leads to a deterministic algorithm.You probably already see the problem here. If then the running time of the deterministic procedure is .That is, of course, terrible running time.On the other hand, if is a constant or even up to , then the resulting running time will stay polynomial, and everyone is happy. In the next section we will see that with an additional assumption, we can “decrease” the seed length from to bits.3 Pairwise Independent Seed
We start off with a definition.k-wise Independent Family. Let be a set of random variables. We say that is a k-wise independent family if for any subset of variables , and values that is, any subset of random variables from is fully independent. The family is called pairwise independent family when .What this definition have with our settings? Observe that up until now we implicitly assumed that the algorithm needs its coins to be fully independent. That is, if we think of as a series of Bernoulli RVs then we actually require to be t-wise independent family, which is a much stronger property compare to the pairwise independence property. If we relax that requirement and assume that the algorithm only needs its coins to be pairwise independent, then there is a way (described in next section) to construct pairwise independent bits using only fully independent bits. That construction can be “embedded” into our algorithm such that we ultimately end up with a procedure that only requires fully independent seed. Applying the derandomization method from previous section will result with a deterministic algorithm that will still run in time.Of course, the aforementioned derandomization method is valid only if the assumption of pairwise independent seed doesn’t break the correctness analysis of the randomized algorithm.4 Stretching the Seed
Suppose we have fair fully independent coins, we want to construct a method to generate from them fair pairwise independent bits. The following claim shows such construction.Suppose we have fully independent Bernoulli random variables, each with probability . Fix them in some arbitrary order to get a (random) vector of length . Let be the set of all possible sums modulo 2 of those RVs and note that , then is a family of pairwise independent bits.To prove that we start with a very basic lemma.Let be two independent random variables, let then . Moreover, is independent from and from .For any thus . Next w.l.o.g we prove that independent from . Take any . In case then so and are independent. And in case that then similarly we get which conclude the proof.Now we prove the claim from above.Take two different variables and , and let , we want to show that and are independent. Obviously, we only care about the set of indices which are non-zero in the vectors and . Let these sets be respectively. Denote , and where summation over empty set is defined as the constant (all the operations in the proof are modulo 2). Note that any pair of variables from are independent because they defined on mutually disjoint set of indices. Moreover, by the lemma from above, each of them if it is not the constant zero then is distributed as . When plugging-in the new notations we get Because there must be at most one variable from which may be constant. Therefore, no matter which it is (if any), either or is a sum of two non-constant variables. W.l.o.g let it be , then it has the component which does not appear in and can flip the result of the sum with probability regardless of what happen anywhere else, therefore is independent of , and that completes the proof.Last one remark. In our settings the randomized algorithm either return a solution or says “failed”, if we have a polynomial procedure to validate a solution we can generalize the settings to the case when the algorithm always output a solution, and then we verify it to determine if it is “succeeds” case of “failed” case. -
Comparing Chernoff - Hoeffding bounds
tags:Comparing Chernoff - Hoeffding bounds Computer science topics over lunchComparing Chernoff - Hoeffding bounds
1 The Definitions and Motivation
Hoeffding and Chernoff bounds (a.k.a “inequalities”) are very common concentration measures that are being used in many fields in computer science. A concentration measure is a way to bound the probability for the event in which the sum of random variables is “far” from the sum of their means.For example: suppose we have (fair) coins to toss and we want to know what is the probability that the total number of heads (i.e sum of indicators) will be “far” from half of the tosses (which is the sum of their means), say that either or . Chernoff’s and Hoeffding’s bounds can be used to bound the probability for that to happen.Both bounds are similar in their settings and their results, and sometimes it is not clear which bound is better for a given setting; maybe even both bounds are equivalent. In this post we will try to get an intuition which bound is stronger (and when).Note that each bounds have several common variations and we will discuss only the ones that are stated below. Let’s start with the first bound, a multiplicative version of Chernoff’s bound.Chernoff bound. Let be a collection of independent random variables ranging in , denote and let , then for anyHoeffding bound. Let be independent random variables ranging in where , denote and let , then for any :2 Writing Hoeffding’s bound as a Chernoff’s bound
In first glance it seems that we cannot compare between the definitions, mostly because this small technical issue: Hoeffding’s bound allows the random variables to be in any close interval rather than . The solution for that is to scale and shift the variables to make them takes values in . We will start with exactly that, and then transform Hoeffding’s inequality into “Chernoff’s”.So for any , denote and let . Observe that . Clearly, now the range of the variables is so we can write Hoeffding’s bound in terms of ’sWhere the inequality in the middle of the process is where we apply Chernoff’s bound with , note that there is an implicit assumption here that .So we managed to formulate Hoeffding’s bound in Chernoff’s settings, ending with a very messy formula. In order to explore the behavior of the bounds further, we will simplify the analysis by adding another assumption: that .3 Which bound to used?
Now we assuming that . The restriction from previous section that is now holds whenever , which make sense because Chernoff’s bound, as we defined it, only concerned with deviations that are up to .Next, the term we got for Hoeffding is simplified further into Now easy to compare between the bounds. With Hoeffding we can achieve bound of and with Chernoff , it just left to compare between and . If then Chernoff is stronger and vise versa. We conclude that none of the bounds is always preferred upon the other (which is not so surprising), and the answer to the question “which one to use” depends on the parameters of the distribution in hand.4 Chernoff bound is tight!
One surprising fact about Chernoff’s bound is that in some cases it is tight (i.e. gives a lower bound). The theorem below is taken from these notes (see the link for the full proof).Let be i.i.d random variables ranging in with , denote and let .
If , then for any If , then for anyNote the differences between that regime and the one from the definition at the beginning of the post: in this theorem the variables are i.i.d (rather than only independent) and they are discrete. -
Introduction to Hypergraphs
tags:Introduction to Hypergraphs Computer science topics over lunchIntroduction to Hypergraphs
In this post, I will discuss basic definitions and theory related to hypergraphs and cut sparsifiers. I will start from the basic definitions of Graphs, then generalize these definitions to Hypergraphs. Later, I will discuss some related theory about Cut-Sparsifiers.1 Basic Definitions in Graphs
Let’s start from the very beginning - graphs. Graphs are fundamental objects in computer science, and they are used to model relations between objects. Formally, a graph is a tuple of two sets, and and a function . is the set of vertices (i.e. the elements), usually denoted as , and is a set of edges between those vertices (i.e. indicating which elements belongs to the relation the graph represents). An edge is just a set of two vertices, that is . The function assigns a weight to every edge in the graph (we will focus on non-negative weights). For instance, we can model friendships in Facebook as a graph, the vertices will be all the users in Facebook, and there will be an edge between any pair of users if they are “friends” of each other.A cut in a graph is a partition of into two sets, . We say that an edge cross the cut defined by if and only if and , that is, the edge “touches” both parts of the graph. Now we can talk about the weight of the cut, that is, if we have a cut that is defined by and a weight function then, in words, the weight of a cut is the sum of weights of all edges that cross it.2 Generalizing to Hyper-Graphs
The model of a graph, as defined above, can’t be used to describe non binary relationships. For example, say we want to model Facebook groups via a graph; the only way to do that is by including in the set of vertices also any group in Facebook, and then connecting each user to any of its groups with an edge. The main issue with such construction is that the vertices represents both users and facebook-groups. In order to avoid such ambiguity we can use a richer model, we can use Hypergraphs.Hypergraphs are generalization of graphs in the sense that edges may be of arbitrary size. Meaning that now . Going back to our example, we can model Facebook groups by the graph when is the set of all users, and any group in Facebook will be an edge (that notation stands for the Power Set of ) such that contains the users belongs to that group.Here is another example, in purely mathematical form, let , which is a valid hypergraph over five vertices and with two edges: and .We also require the domain of the weight function to be (rather than in the case of regular graphs). That requirement allows us to apply the same definitions of cuts and cut weight as they were phrased for regular graphs.Usually we are interested in family of hypergraphs with limited size, that is, hypergraphs where each edge is of size at most . Such hypergraphs are said to be r-uniform.3 Cuts Sparsification
We move to define Cut-Sparsifiers: Let . Given a hypergraph and a weight function , we say that a hypergraph is -cut-sparsifier of if and the set may be any set in . The subscript “ ” in the function indicates that the weights are over the hypergraph (and similarly with and ).It is not part of the definition, but the goal is to find cut-sparsifier that shrink the number of edges, that is, with the smallest possible. Whereas in regular graphs it is understood that we want to minimize the number of edges, in hypergraphs we should also consider the size of the edges in . That is, the quality of the sparsifier will be measured also by the size of the edges in the resulting graph. For that we define the total edge size of a hypergraph to be .4 Upper & Lower Bounds for Sparsification
For regular graphs, we already know how to reduce the number of edges to be for any . That is surprising, because no matter how many edges there are in the original graph, which can be up to , there is an algorithms that can reduce the number of edges to , while maintaining approximately the same weights for all possible cuts in the graph. Moreover, that algorithm find the cut-sparsifier in polynomial time.Later results show that this upper bound is also a lower bound, that is, there are graphs that cannot be reduced into less that edges.However, when working with hypergraphs it is not quite clear if one can reduce the total edges size of the graph to be even order of . Think about it, potentially the number of edges in a hypergraph can be , so can be considered quite small for such hypergraphs.An interesting result from 2015, showed lower bound of edges for r-uniform hypergraphs (assuming that ), which, when converting to total edges size is actually .The question that one can ask now is, can we do better? Is there an algorithm that can construct a cut-sparsifier for hypergraphs with smaller total edges size?That is, actually, an open question which is studied nowdays.
Tags
Jekyll::Drops::SiteDrop